Complete documentation and usage examples. Web sign chart of the derivative is very useful for findig the maxima, minima, and saddle points of a function. Recognize that iff(x) is positive for one value in an interval, then f(x) is positive for all values. Web here are the basics of how to create a sign chart and how to use it to solve inequalities. For example, of the type (ax+b) (gx+h) (px+q) (sx+t)>0 it could also be less than or less than or equal or greater than or.
Web graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Recognize that iff(x) is positive for one value in an interval, then f(x) is positive for all values. This method is based on the following: This will divide the domain into intervals. Finding decreasing interval given the function.
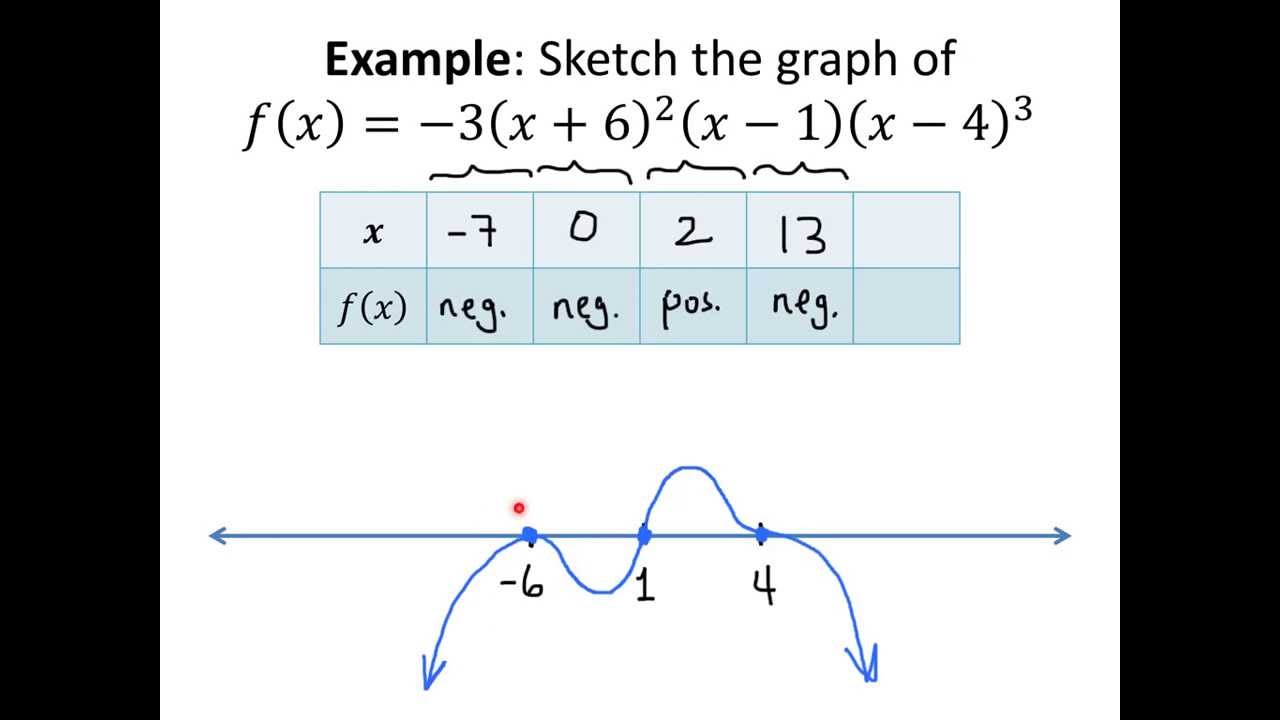
Web sign chart of the derivative is very useful for findig the maxima, minima, and saddle points of a function. The intervals where a function is increasing (or decreasing) correspond to the intervals where its derivative is positive (or negative). Begin by finding all special values of the polynomial. 1 a linear factor, ax + b, will be zero at one point (x = b a) and will be positive on one side of the zero and negative on the other. The f(𝑥) sign diagram displays where the function outputs are positive or negative.
What is a sign chart in calculus?
How to Understand Sign Diagrams
Sign Chart Math A Visual Reference of Charts Chart Master
Sign chart calculus qustmama
How to Understand Sign Diagrams
Solving Inequalities Using sign chart Calculus 1 YouTube
How to Understand Sign Diagrams
How to Understand Sign Diagrams
How to Understand Sign Diagrams
How to Understand Sign Diagrams
Since sign chart is based on bolzano's theorem. Learn how to draw a sign chart here. Finding increasing interval given the derivative. The f(𝑥) sign diagram displays where the function outputs are positive or negative. Web summary of sign analysis technique 1. Web they provide a concise way to understand the sign of a function within specific intervals. Web here are instruction for establishing sign charts (number line) for the first and second derivatives. 1 a linear factor, ax + b, will be zero at one point (x = b a) and will be positive on one side of the zero and negative on the other. Web graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Get a grid of sign charts for a function and its first and second derivatives. Recognize that iff(x) is positive for one value in an interval, then f(x) is positive for all values. Web sign chart is used to solve inequalities relating to polynomials, which can be factorized into linear binomials. Begin by finding all special values of the polynomial. Web signs and sign charts the other method is to use a sign chart with the signs of the factors. For example, of the type.
Web Review How We Use Differential Calculus To Find The Intervals Where A Function Increases Or Decreases.
Web an inflection point (or point of inflection) is the point at which the concavity of the graph changes sign. Web sign chart of the derivative is very useful for findig the maxima, minima, and saddle points of a function. Begin by finding all special values of the polynomial. Recognize that iff(x) is positive for one value in an interval, then f(x) is positive for all values.
For Example, Of The Type (Ax+B) (Gx+H) (Px+Q) (Sx+T)>0 It Could Also Be Less Than Or Less Than Or Equal Or Greater Than Or.
Get a grid of sign charts for a function and its first and second derivatives. Find critical points get 3 of 4 questions to level up! By examining the intervals where the function is positive, negative, or zero, sign charts aid in identifying critical points, determining the behavior of. Download an example notebook or open in the cloud.
Web Sign Chart Is Used To Solve Inequalities Relating To Polynomials, Which Can Be Factorized Into Linear Binomials.
The intervals where a function is increasing (or decreasing) correspond to the intervals where its derivative is positive (or negative). Web signs and sign charts the other method is to use a sign chart with the signs of the factors. Web here are instruction for establishing sign charts (number line) for the first and second derivatives. This method is based on the following:
The Intervals You Want Are (−∞, −2) ( − ∞, − 2), (−2, 3) ( − 2, 3), And (3, ∞) ( 3, ∞).
1 a linear factor, ax + b, will be zero at one point (x = b a) and will be positive on one side of the zero and negative on the other. Learn how to draw a sign chart here. (ax +b)(gx + h)(px + q)(sx + t) > 0. Intervals on which a function is increasing or decreasing.